ganzrationale Funktionen

Quelle: https://www.sciencealert.com/dragging-out-the-coronavirus-epidemic-is-important-in-saving-lives

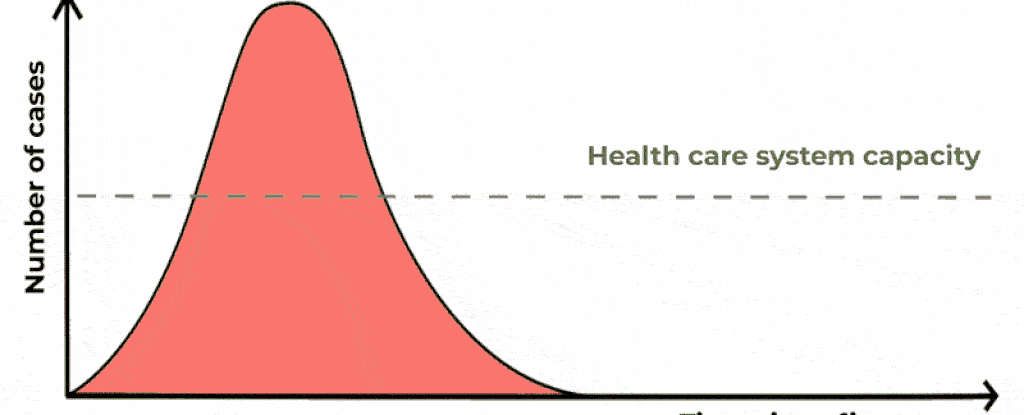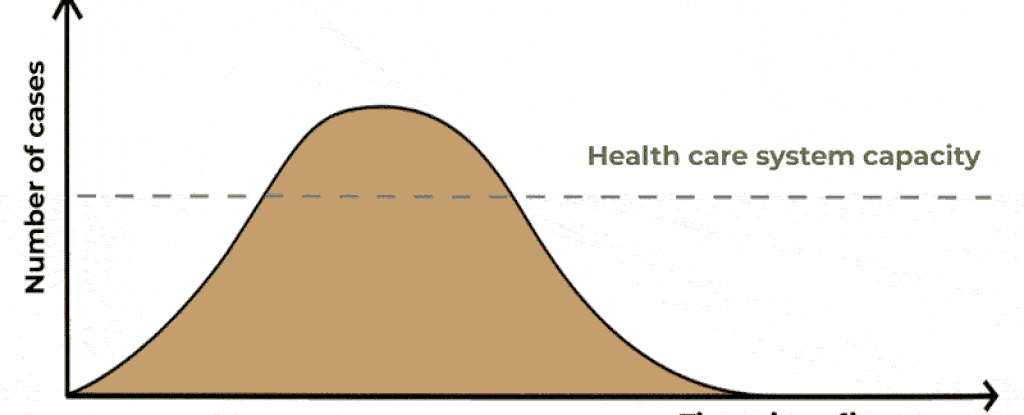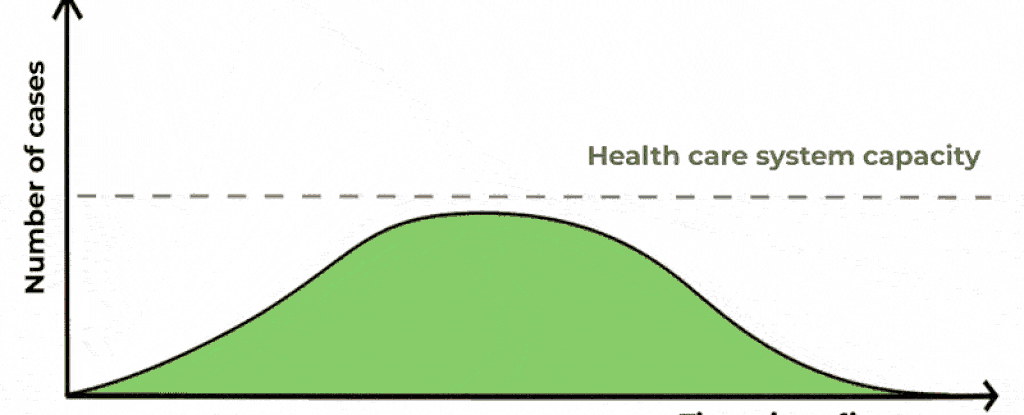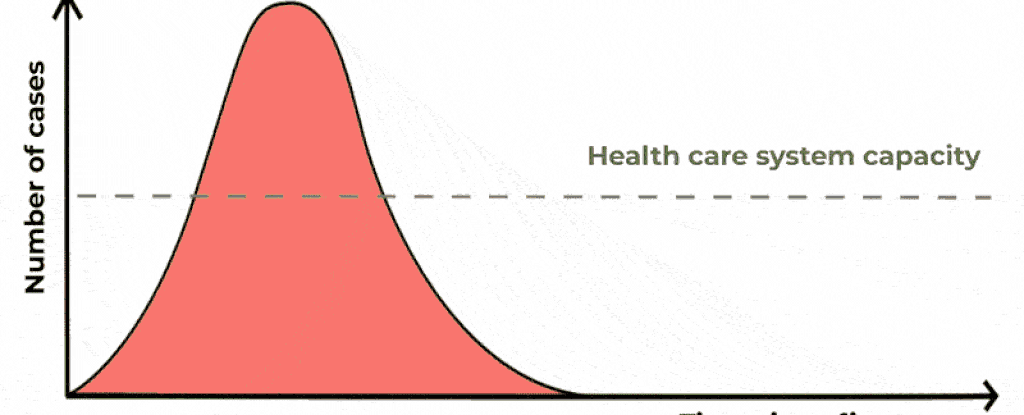
"Flatten the curve" ist die Aufforderung, sich vorsichtig zu verhalten um die Corona-Ansteckung in der Bevölkerung gering zu halten:
Die "Kurve" ist dabei der Graph der aktuellen Infektionsfälle. Ziel ist es, ihn unterhalb der Linie zu halten, die der Kapazität unseres Gesundheitssystems entspricht.

Die Graphen erinnern vielleicht etwas an quadratische Parabeln, aber wenn du genau hinschaust, erkennst du, dass das nicht so ganz passen würde.
Quadratische Funktionen haben halt grundsätzlich immer dieselbe Form - abgesehen von Streckung und Stauchung.
Ganzrationale Funktionen sind eher biegsam - ähnlich wie Draht: Ihr Graph kann immer wieder in eine andere Richtung gehen.


Normalform der ganzrationalen Funktion:
$$f(x)=a_n\cdot x^n+a_{n-1}\cdot x^{n-1}+...+a_1x+a_0.$$

Gleichungen:

Checklist ganzrationale Gleichungen - das ganze Paket: pdf

Training faktorisierte Form und Satz vom Nullprodukt (Gleichungen lösen ohne viel Rechnen!): pdf
Training Gleichungen lösen durch Ausklammern: pdf

Check Gleichungen lösen durch Ausklammern: pdf
Check ganzrationale Gleichungen - teilweise faktorisierte Gleichungen und Satz vom Nullprodukt: pdf

Training ganzrationale Gleichungen - teilweise faktorisierte Gleichungen und Satz vom Nullprodukt: pdf

Training ganzrationale Gleichungen: externer Link: (Klett)

Check ganzrationale Gleichungen - Substitution: pdf

Funktionen:

Check ganzrationalen Funktion (faktorisierte Form): pdf

Erklärfilm Skizzieren des Graphs einer ganzrationalen Funktion (faktorisierte Form): mp4

Erklärfilm ganzrationale Gleichungen - mit Vorarbeiten (teilweise schon faktorisiert): mp4

Arbeitsblatt zur Einführung in die faktorisierte Form bei ganzrationalen Funktionen pdf

Arbeitsblatt zur faktorisierten Form bei ganzrationalen Funktionen (Gleichung aus Graph ablesen, Nullstellenberechnung und Skizze des Graphen) pdf, Lösung dazu: pdf, ähnliches Arbeitsblatt zum weiteren Training: pdf, Lösung dazu: pdf

Check Kubische Funktionen (=Funktionen vom Grad 3) ohne Differentialrechnung: pdf

Check Funktionen vom Grad 4 ohne Differentialrechnung: pdf

Check Funktionen in der faktorisierten Form: pdf

Autobahnfahrt (eingekleidete Aufgabe ganzrationale Funktionen): pdf

Wetterballons (eingekleidete Aufgabe ganzrationale Funktionen): pdf

Check Differentialrchnung: ganzrationale Funktionen ableiten: pdf

Check Kubische Funktionen (=Funktionen vom Grad 3): pdf

Check Funktionen vom Grad 4: pdf

Check Steckbriefaufgaben kubische Funktion: pdf

Check Integralrechung bei ganzrationalen Funktionen: pdf

Check Anwendungen Differentialrechnung - Kinematik (Weg, Geschwindigkeit, Beschleunigung): pdf


einige grundlegende Begriffe im Glossar: ganzrationale Funktion, Leitkoeffizient, Grad, Potenzfunktionen, faktorisierte Form bei kubischen Funktionen, faktorisierte Form , Fernverhalten, Horner-Schema, Polynomdivision, Potenzregel der Integralrechnung, Potenzregel der Differentialrechnung


Für die Übersicht, was man in diesem Zusammenhang alles können kann,
gibt es Checklists mit Links zu Trainingsmöglichkeiten:

Checklist ganzrationale Funktionen: pdf

ökonomische Anwendungen ganzrationaler Funktionen

Übersicht ökonomische Anwendungen: pdf
Checklist ökonomische Anwendungen kubischer Funktionen: pdf

Training Steckbriefaufgaben (Erlös-, Kosten-, Gewinnfunktion): pdf

Standardaufgaben (Beispiele und Lösungen): Gewinnzone, Extrempunkte (kubische Funktion), Extrempunkte (kubische Funktion) Bsp. 2, Wendepunkte (kubische Funktion) Bsp. 1, Wendepunkte (kubische Funktion) Bsp. 2